0x5f3759df

Scene in OpenArena, from Wikipedia

這不是什麼亂碼，這串神奇的數字可是無數經典遊戲的幕後推手：「平方根倒數速算法」中的魔法。上圖是 OpenArena 的遊戲畫面，其中的光照效果就是藉由該演算法實現的。今天 google 到此演算法，覺得十分有趣，想知道這是怎麼做到的呢？本篇為平方根倒數速算法的介紹及分析筆記。

緣起

電腦遊戲由 2D 橫向捲軸發展至 3D 第一人稱視角時，因為要繪製隨玩家操縱而隨時改變的視角，對及時運算的要求大幅提升。除了等待硬體升級，程式設計師們也絞盡腦汁地設計加快運算的演算法，尤其對一些基本、多次使用的函式。計算平方根的倒數就是一例。

十幾年前，一位雷神之鎚 III (Quake III Arena) 的程式設計師，寫下了這段 C 語言代碼

float Q_rsqrt( float number )
{
  long i;
  float x2, y;
  const float threehalfs = 1.5F;

  x2 = number * 0.5F;
  y  = number;
  i  = * ( long * ) &y;                         // evil floating point bit level hacking
  i  = 0x5f3759df - ( i >> 1 );                 // what the fuck?
  y  = * ( float * ) &i;
  y  = y * ( threehalfs - ( x2 * y * y ) );     // 1st iteration
  // y  = y * ( threehalfs - ( x2 * y * y ) );     // 2nd iteration, this can be removed
  return y;
}

雷神之鎚 III 在 1999 年上市，這段代碼直到 2005 年才公開，但早在 2002 年就已經在 Usenet 論壇間流傳。這是牛頓法 (Newton’s method) 計算平方根的倒數的實作，但是速度比當時編譯器內的數值方法快了四倍。其巧妙之處，就在於那個 0x5f3759df。

原理

先從數學上看這個問題：給一個實數 x，欲求 1/\sqrt{x}。

這相當於給一常數，求 f(y) = 1/y^2 - x 的正實根，一般情況我們必須用數值方法求解。

艾薩克・牛頓爵士曰：一函數之實根可由一起始點函數的切線與橫軸交點反覆迭代得之。數學如此表示：

y_{n+1} = y_n + \frac{f(y_n)}{f'(y_n)}

y_n 為第 n 次迭代的結果，將上式代入我們感興趣的平方根倒數函數，化簡就得到了程式碼第 12 行

y_{n+1} = y_n + y_n(\frac{3}{2} - \frac{x}{2}y_n^2)

上面的程式碼果然是牛頓法，而且只用了一次迭代（本來想用第二次被注解掉了！）牛頓法向來以收斂快速行走江湖，對於電腦圖學要的精準度來說，通常幾次迭代就足夠。但一次到位也實在太神奇了，這說明初始值 y_0 選得非常好，究竟是什麼初始值能讓牛頓法一次迭代就給出如此精確的解？

答案就在程式碼第 10 行，該程式設計師並下了一個很好的註解。

分析

這個速算法是針對 IEEE 754-1985 的 32 位元浮點數 (float) 開發的，要分析必須先了解該浮點數的結構：

Sign (s) Exponent (E) Mantissa (M)
bit 31 bit 30-23 bit 22-0

E 看做是一個 0-255 的非負整數，加上一個 127 的 bias 以表示 0 和 1 之間的實數。而 M 可看作 (0-2^{22})/2^{23} 的實數，表示 x 的小數點以下的有效位數。因此，給定的常數 x，在該結構下表示如下

x = (-1)^s(1+M)2^{e}

其中 e = E-127。而我們要求的平方根倒數，可以表示成

y = \frac{1}{\sqrt{x}} = \frac{1}{\sqrt{1+M}}2^{-e/2}

程式碼第 10 行選了一個神奇的數字減去向右偏移一個位元的 x，就成了 x 的平方根倒數初始值 y_0。這招藏了好幾步在裡面：

  • 開根號取倒數，等於指數部分乘以 -1/2。這邊把浮點數當整數，用 bit operation (指數 >>1 相當於除以 2，減法取了倒數) 做掉了
  • 神秘常數保留 mantissa 的精準度

假設有一個常數 R 可以用以作上述運算近似平方根倒數，以 0|E|M 表示 32 位元的非負常數 x，0|R1|R2 表示 32 位元的魔術常數 R，我們想知道為什麼 y_0 = R - (x\gg1) 是一個好的初始值？

先從討論 x 最簡單的一種形式開始

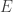E 為偶數

E 如果為偶數，代表其 8 個位元的最後一位為 0，那麼 x 向右偏移一位，E 就不會使 M 溢位。在這例子下，y_0 指數位元運算如下

R_1 - \lfloor E/2 \rfloor = R_1 - E/2 = R_1 - \frac{e+127}{2} = R_1 - 64 - d

因為 e=E-127 為奇數，可用 2d+1 代入得到上述關係式。同時，我們要求這個新的差值必須是正數。

y_0 的 mantissa 可以寫作 R_2 - \lfloor M/2 \rfloor，由於 floor function 的影響最多只有 2^{-24}，這邊可以直接忽略不計。因此，初始值 y_0 以下列表示

y_0 = (1 + R_2 - M/2)2^{(R_1 - 64 - d) - 127} = (1 + R_2 - M/2)2^{R_1 - 191 - d}

如果 R_2 - M/2 為正，上式可換做 y_0 = (2 + 2R_2 - M)2^{R_1 - 192 - d}。

反之如果 R_2 - M/2 為負，則會向指數位元借位（因前述正數要求保證可借），可寫成以下關係式

y_0 = (1 + (1 + R_2 - M/2))2^{(R_1 - 191 - d) - 1}= (2 + R_2 - M/2)2^{R_1 - 192 - d}

因此不論 R_2 - M/2 的正負，指數部分在此統一了，Mantissa 的部分可以寫作 R_2 和 M 的關係式，整理如下：

y_0 = (2 + \beta^{R_2}_M)2^{R_1 - 192 - d}

就此，我們也用位元的概念表示初始解 y_0，現在我們關心的就是它和 analysitic solution y 的誤差有多大。同樣的，我們用 d 代換

y = \frac{1}{\sqrt{(1+M)}}2^{-e/2} = \frac{1}{\sqrt{2}\sqrt{1+M}}2^{-d}

相對誤差 |\frac{y - y_0}{y} | = |\epsilon_0(M,R)| 在絕對值內的項次可化簡如下

\epsilon_0(M,R) = 1 - \sqrt{2}\sqrt{1+M}(2+\beta^{R_2}_M)2^{R_1-192}

在 E 為偶數的前提下，現在誤差和 d 徹底擺脫關係了，但是和 R 和 M 形成了一組關係式。如果我們希望魔術常數能提供誤差範圍在 0.125 內的近似，可以寫下不等式

\frac{1}{8} > \max_{M\in \mathbf{I}} |\epsilon_0| \geq |\epsilon_0(0,R_2) | = |1 - (1+R_2)2^{R_1-190.5}|

展開可得

\frac{9}{8} \geq \frac{9}{8(1+R_2)} > 2^{R_1 - 190.5} > \frac{7}{8(1+R_2)} > \frac{7}{16}

上述關係式因為 (1 + R_2) \in [1, 2) 成立，而滿足該關係式的正整數 R_1 剛好就只有一個：190，該數用 16 進位表示為 0xbe。由於 0xbe 寫在 R_1 的位置，換作 R 還要加上第一位 sign bit，所以往右偏一位，魔術數字的開頭就此定讞：0x5f。

小結

上述所討論的情況，僅能解釋 E 為偶數的情況。但事實上，如果用此套路分析 E 為奇數時，會得到一樣的結果。選擇 0x5f 為魔術數字 R 的開頭，在於它能適度的減少近似值的相對誤差。

剩下來的問題就是 3759df，也就是如何對魔術數字的 mantissa R_2 做最佳化？限於篇幅，不多細談，關於本演算法，更多細節與實驗可以參考時任普渡大學博士生 Chris Lomont 的論文。

平方根倒數速算法被研究透徹了，在現代的計算機結構上還有更多針對平台最佳化的解法，然而，0x5f3759df 的作者卻一直不可考。他是誰，究竟是怎麼樣的神來一筆，讓他寫下了如此簡潔動人的程式？那又是另一個令人感興趣的故事。

Reference

Leave a comment